For reference, a derivation of a variational approximation for linear regression following (Ormerod 2008) and (Ormerod and Wand 2010).

Recall the evidence lower bound is given by \[ \begin{aligned} \ln p(y|\theta) &\geq \mathcal{L}(y|\theta;q) \\ &= \mathbb E_q[\ln p(y,\theta) - \ln q(\theta)] \\ &= \mathbb E_q[\ln p(y|\theta)] + \mathbb E_q[\ln p(\theta)] + \mathbb H_q[\theta]. \end{aligned} \]

The model we are interested in is \[ \begin{aligned} y|\beta,\sigma^2 &\sim N(X\beta, \sigma^2 I_n) \\ \beta &\sim N(\mu_0,\Sigma_0) \\ \sigma^2 &\sim IG(a_0, b_0). \end{aligned} \]

Suppose we specify a parametric approximating density \(q(\beta,\sigma^2;\xi) = q(\beta;\xi_\beta)q(\sigma^2;\xi_\sigma)\) where \[ \begin{aligned} q(\beta;\xi_\beta) &= N(\beta|\mu_\beta, \Sigma_\beta) \\ q(\sigma^2;\xi_\sigma) &= IG(\sigma^2|a_{\sigma^2}, b_{\sigma^2}). \end{aligned} \]

We then have the following lower bound \[ \mathcal{L}(y|\theta;q) = \mathbb E_q[\ln p(y|\beta,\sigma^2)] + \mathbb E_q[\ln p(\beta)] + \mathbb E_q[\ln p(\sigma^2)] + \mathbb H_q[\beta] + \mathbb H_q[\sigma^2]. \]

The components are \[ \begin{aligned} \mathbb E_q[\ln p(y|\beta,\sigma^2)] &= -\frac{1}{2}\left\{n\ln(2\pi) + \mathbb E_q[\ln\sigma^2] + \mathbb E_q[\sigma^{-2}]\mathbb E_q[(y - X\beta)^\top(y - X\beta)]\right\} \\ &= -\frac{1}{2}\left\{n\ln(2\pi) - \ln(b_{\sigma^2}) + \psi(a_{\sigma^2}) + \frac{a_{\sigma^2}}{b_{\sigma^2}}\left[(y-X\mu_\beta)^\top(y-X\mu_\beta)+\text{tr}(X^\top X\Sigma_\beta)\right]\right\}\\ \mathbb E_q[\ln p(\beta)] &= -\frac{1}{2}\left\{d\ln(2\pi) + \ln|\Sigma_0| + \mathbb E[(\beta - \mu_0)^\top\Sigma_0^{-1}(\beta-\mu_0)]\right\}\\ &= -\frac{1}{2}\left\{d\ln(2\pi)+\ln|\Sigma_0| + (\mu_\beta-\mu_0)^\top\Sigma_0^{-1}(\mu_\beta-\mu_0) + \text{tr}(\Sigma_0^{-1}\Sigma_\beta)\right\} \\ \mathbb E_q[\ln p(\sigma^2)] &= a_0\ln(b_0)-\ln\Gamma(a_0)+(a_0+1)\mathbb E_q[\ln(\sigma^{-2})] - b_0\mathbb E_q[\sigma^{-2}] \\ &= a_0\ln(b_0)-\ln\Gamma(a_0)-(a_0+1)(\ln(b_{\sigma^2}) - \psi(a_{\sigma^2}))- b_0\frac{a_{\sigma^2}}{b_{\sigma^2}} \\ \mathbb H_q[\beta] &= \frac{1}{2}\left[d(1 + \ln(2\pi)) + \ln|\Sigma_\beta|\right]\\ \mathbb H_q[\sigma^2] &= a_{\sigma^2} + \ln(b_{\sigma^2}) + \ln\Gamma(a_{\sigma^2}) - (a_{\sigma^2} + 1)\psi(a_{\sigma^2}) \end{aligned} \]

where we have used the following identities

\[ \begin{aligned} \mathbb E_q[\beta^\top\Sigma_0^{-1}\beta] &= \mu_\beta\Sigma_0^{-1}\mu_\beta + \text{tr}\left(\Sigma_0^{-1}\Sigma\right)\quad\text{(quadratic form)}\\ \mathbb E_q[\sigma^{-2}] &= \frac{a_{\sigma^2}}{b_{\sigma^2}} \quad \text{(expectation of gamma r.v)}\\ \mathbb E_q[\ln(\sigma^{-2})] &= \ln(b_{\sigma^2}) - \psi(a_{\sigma^2}) \quad\text{(expectation of log gamma r.v.)}. \end{aligned} \]

For optimisation, the derivatives are \[ \begin{aligned} D_{\mu_\beta}\mathcal{L}(y|\theta;q) &= -\frac{1}{2}\left(\frac{a_{\sigma^2}}{b_{\sigma^2}}X^\top(y - X\mu_\beta) - \Sigma^{-1}_0(\mu_\beta-\mu_0)\right) \\ D_{\Sigma_\beta}\mathcal{L}(y|\theta;q) &= -\frac{1}{2}\left(\frac{a_{\sigma^2}}{b_{\sigma^2}}X^\top X + \Sigma_0^{-1} - \Sigma_\beta^{-1}\right)\\ D_{a_{\sigma^2}}\mathcal{L}(y|\theta;q) &= 1 + \left(a_0 + n/2 - a_{\sigma^2}\right)\psi^\prime(a_{\sigma^2}) - \frac{1}{b_{\sigma^2}}\left(b_0 + \frac{(y - X\mu_\beta)^\top(y - X\mu_\beta) + \text{tr}(X^\top X\Sigma)}{2}\right)\\ D_{b_{\sigma^2}}\mathcal{L}(y|\theta;q) &= \left(b_0 + \frac{(y-X\mu_\beta)^\top(y-X\mu_\beta) + \text{tr}(X^\top X \Sigma)}{2}\right)\frac{a_{\sigma^2}}{b_{\sigma^2}^2} - \frac{\left(a_0 + \frac{n}{2}\right)}{b_{\sigma^2}} \end{aligned} \] using \[ \begin{aligned} D_X \ln|X| &= (X^{-1})^\top\\ D_X \text{tr}(AXB) &= A^\top B^\top \end{aligned} \]

This results in fixed-point updates \[ \begin{cases} \Sigma_\beta \leftarrow \left(\frac{a_{\sigma^2}}{b_{\sigma^2}}X^\top X + \Sigma_0^{-1}\right)^{-1}\\ \mu_\beta \leftarrow \Sigma\left(\frac{a_{\sigma^2}}{b_{\sigma^2}}X^\top y + \Sigma_0^{-1}\mu_0\right)\\ a_{\sigma^2} \leftarrow a_0 + \frac{n}{2} \\ b_{\sigma^2} \leftarrow b_0 + \frac{(y-X\mu_\beta)^\top(y-X\mu_\beta) + \text{tr}(X^\top X \Sigma)}{2} \end{cases} \]

Example

An R implementation and comparisons with results from Stan are given below.

# Entropy for multivariate normal
mvn_ent <- function(Sigma) {
  (ncol(Sigma)*(1 + log(2*pi)) + log(det(Sigma)))/2
}

# Entropy for inverse gamma
ig_ent <- function(a, b) {
  a + log(b) + lgamma(a) - (a + 1)*digamma(a)
}

# VB for linear regression model
vb_lin_reg <- function(
  X, y, 
  mu0 = rep(0, ncol(X)), Sigma0 = diag(10, ncol(X)), 
  a0 = 1e-2, b0 = 1e-2, 
  maxiter = 100, tol = 1e-5, verbose = TRUE) {
  
  d <- ncol(X)
  n <- nrow(X)
  invSigma0 <- solve(Sigma0)
  invSigma0_x_mu0 <- invSigma0 %*% mu0
  XtX <- crossprod(X)
  Xty <- crossprod(X, y)
  mu <- mu0
  Sigma <- Sigma0
  a <- a0 + n / 2
  b <- b0
  lb <- as.numeric(maxiter)
  i <- 0
  converged <- FALSE
  while(i <= maxiter & !converged) {
    i <- i + 1
    a_div_b <- a / b
    
    Sigma <- solve(a_div_b * XtX + invSigma0)
    mu <- Sigma %*% (a_div_b * Xty + invSigma0_x_mu0)
    y_m_Xmu <- y - X %*% mu
    b <- b0 + 0.5*(crossprod(y_m_Xmu) + sum(diag(Sigma %*% XtX)))[1]
    
    # Calculate L(q)
    lb[i] <- mvn_ent(Sigma) + ig_ent(a, b) +
      a0 * log(b0) - lgamma(a0) - (a0 + 1) * (log(b) - digamma(a)) - b0 * a / b -
      0.5*(d * log(2*pi) + log(det(Sigma0)) + crossprod(mu - mu0, Sigma0 %*% (mu - mu0)) + sum(diag(invSigma0 %*% Sigma))) -
      0.5*(n * log(2*pi) - log(b) + digamma(a) + a / b * (crossprod(y_m_Xmu) + sum(diag(XtX %*% Sigma))))
    
    if(verbose) cat(sprintf("Iteration %3d, ELBO = %5.10f\n", i, lb[i]))
    if(i > 1 && abs(lb[i] - lb[i - 1]) < tol) converged <- TRUE
  }
  return(list(lb = lb[1:i], mu = mu, Sigma = Sigma, a = a, b = b))
}

// lin_reg
data {
  int<lower=1> n;
  int<lower=1> d;
  real y[n];
  matrix[n, d] X;
  vector[d] mu0;
  matrix[d, d] Sigma0;
  real<lower=0> a0;
  real<lower=0> b0;
}

parameters {
  vector[d] beta;
  real sigmasq;
}

model {
  real sigma = sqrt(sigmasq);
  sigmasq ~ inv_gamma(a0, b0);
  beta ~ multi_normal(mu0, Sigma0);
  y ~ normal(X * beta, sigma);
}

library(rstan)
library(MCMCpack)

n <- 50
beta <- c(1, 2, 3)
sigma <- 0.5
x1 <- runif(n)
x2 <- sample(c(0, 1), n, replace = T)
X <- cbind(1, x1, x2)
y <- drop(X%*%beta + rnorm(n, 0, sigma))
D <- data.frame(x1 = x1, x2 = x2, y = y)
mu0 <- rep(0, length(beta))
Sigma0 <- diag(1, length(beta))
a0 <- 1e-2
b0 <- 1e-2

vb_fit <- vb_lin_reg(X, y, mu0 = mu0, Sigma0 = Sigma0, a0 = a0, b0 = b0, tol = 1e-8)

Iteration   1, ELBO = -97.3262155814
Iteration   2, ELBO = -87.2253181794
Iteration   3, ELBO = -87.1217605969
Iteration   4, ELBO = -87.1151041597
Iteration   5, ELBO = -87.1146632789
Iteration   6, ELBO = -87.1146340212
Iteration   7, ELBO = -87.1146320794
Iteration   8, ELBO = -87.1146319505
Iteration   9, ELBO = -87.1146319419

mc_fit <- sampling(lin_reg, refresh = 0, iter = 1e4,
  data = list(n = n, d = 3, X = X, y = y, mu0 = mu0, Sigma0 = Sigma0, a0 = a0, b0 = b0))
draws <- as.matrix(mc_fit)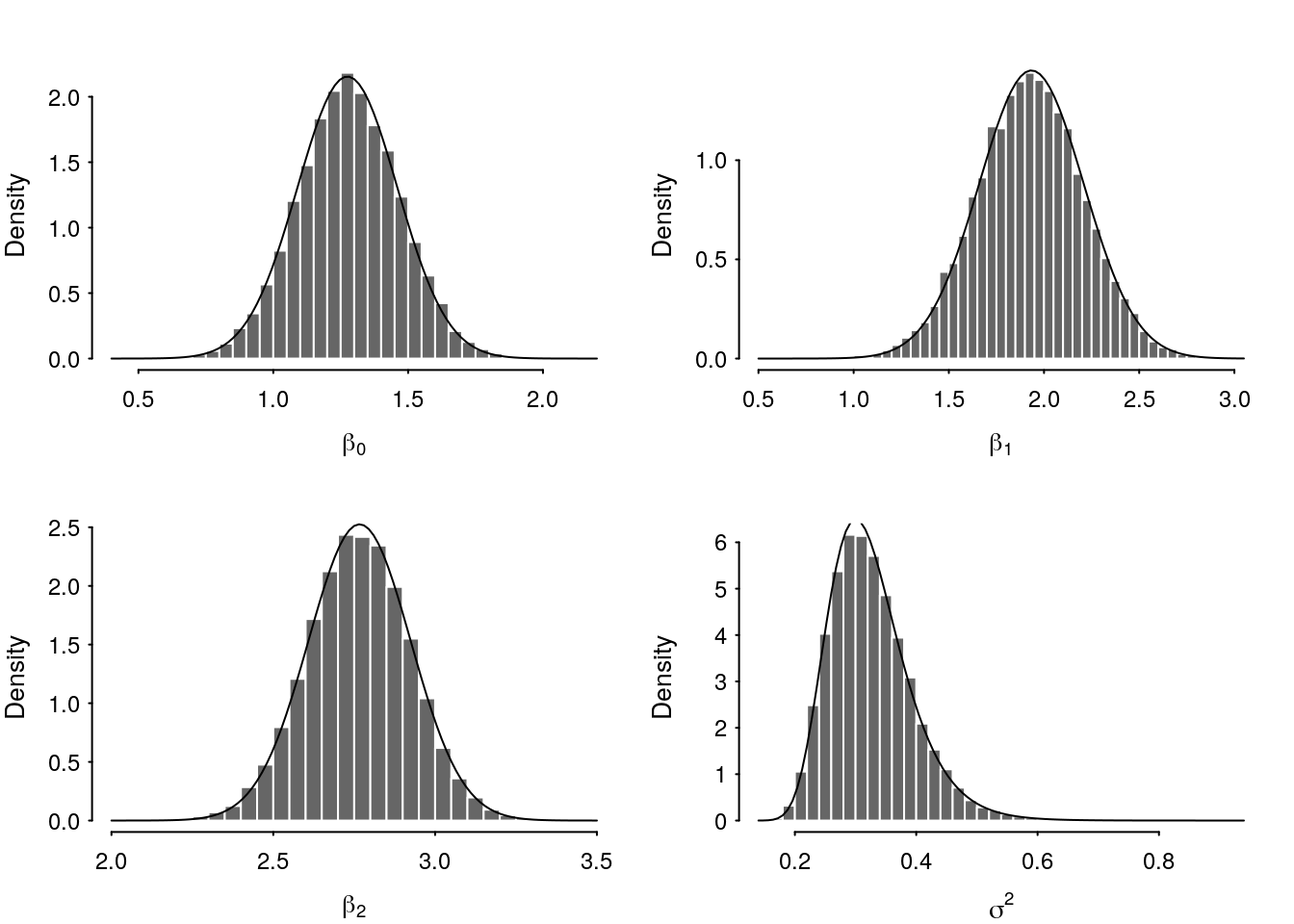

Figure 1: Comparison of variational and HMC posterior densities.

Same data under a different prior.

mu0 <- rep(10, length(beta))
Sigma0 <- diag(0.1, length(beta))
a0 <- 1e-2
b0 <- 1e-2

vb_fit <- vb_lin_reg(X, y, mu0 = mu0, Sigma0 = Sigma0, a0 = a0, b0 = b0, tol = 1e-8)

Iteration   1, ELBO = -96.6398329245
Iteration   2, ELBO = -86.0777933979
Iteration   3, ELBO = -83.4850550434
Iteration   4, ELBO = -78.8496581897
Iteration   5, ELBO = -73.7360282502
Iteration   6, ELBO = -73.0800738730
Iteration   7, ELBO = -73.0558414617
Iteration   8, ELBO = -73.0545704858
Iteration   9, ELBO = -73.0544993784
Iteration  10, ELBO = -73.0544953843
Iteration  11, ELBO = -73.0544951599
Iteration  12, ELBO = -73.0544951473
Iteration  13, ELBO = -73.0544951465

mc_fit <- sampling(lin_reg, refresh = 0, iter = 1e4,
  data = list(n = n, d = 3, X = X, y = y, mu0 = mu0, Sigma0 = Sigma0, a0 = a0, b0 = b0))
draws <- as.matrix(mc_fit)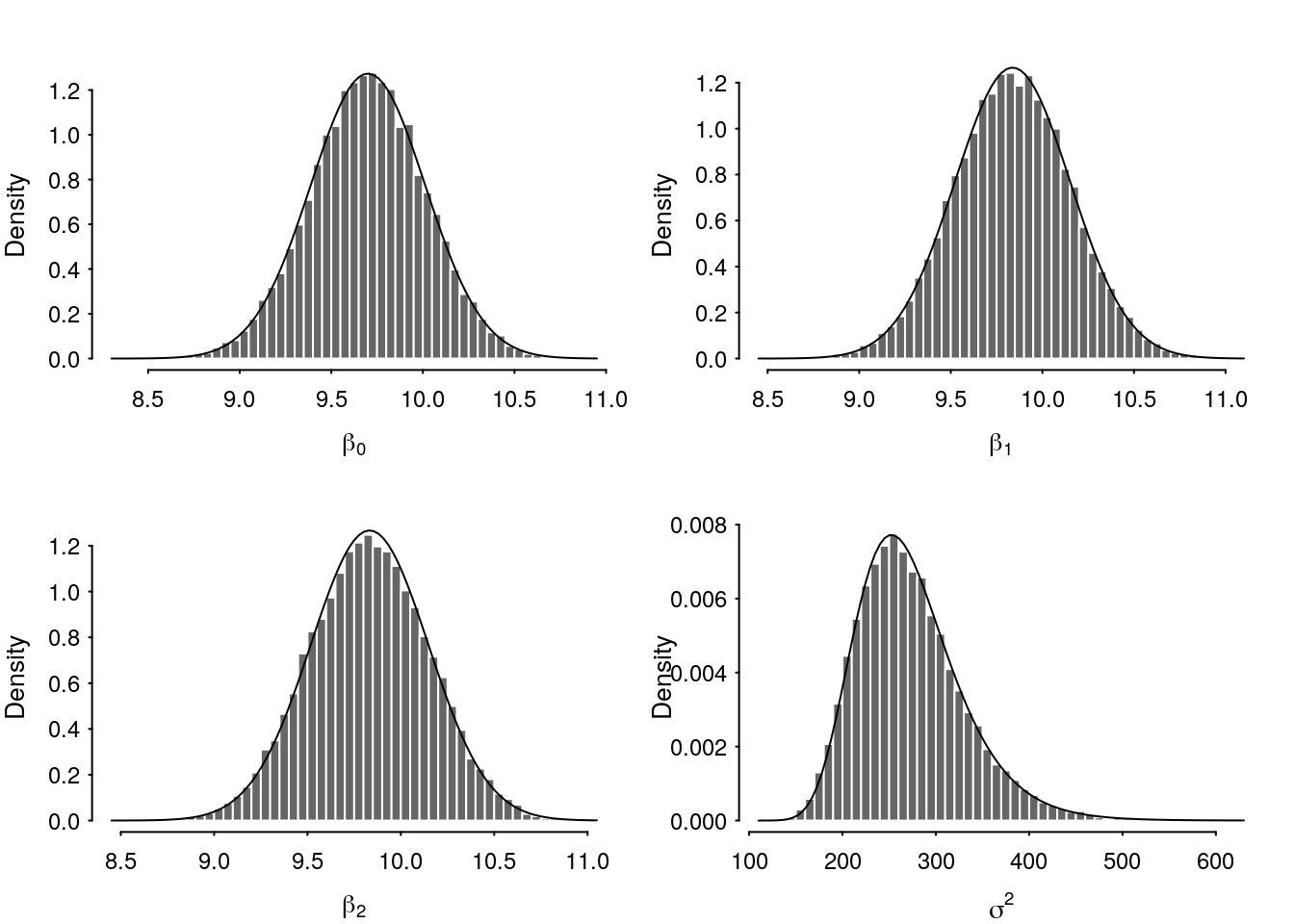

Figure 2: Comparison of variational and HMC posterior densities under strongly informative prior.

---